تصاویری زیبا با موضوع ریاضیات

برای دیدن بقیه تصاویر به ادامه مطلب مراجعه کنید

عکس هایی از هندسه فراکتال

برای دیدن بقیه عکس ها به ادامه مطلب بروید

عدد فی یا عدد مقدس

به گزارش آخرین نیوز، پیشینه توجه به عدد طلایی نه به زمان فیبوناچی بلکه به زمانهای بسیار دورتر می‌رسد.اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کرده‌است. لوکا پاچیولی در سال ۱۵۰۹ میلادی کتابی با عنوان نسبت الهی (The Divine Proportion) تالیف کرد. وی در آن نقاشی‌هایی از لئوناردو داوینچی آورده‌است که پنج جسم افلاطونی را نمایش می‌دهند و در آنها نیز به این نسبت اشاره شده‌است.

روش جالب دانش آموز با ذکاوت«شارل فردریک گاوس»

سال ها پیش در یکی از کلاس های ریاضیات مدارس آلمان، آموزگار برای اینکه مدتی بچه ها را سرگرم کند و به کارش برسد؛ از آنها خواست تا مجموع اعداد از یک تا صد را حساب کنند. پس از چند دقیقه یکی از شاگردان کلاس گفت: مجموع این اعداد را پیدا کرده و حاصل عدد ۵۰۵۰ می شود. با شنیدن این عدد معلم با حیرت فراوان او را به پای تخته برد تا روش محاسبه خود را توضیح دهد. به نظر شما این شاگرد باهوش که بعدها یکی از بزرگ ترین و معروف ترین ریاضیدانان دنیا شد.
چه روشی را به کار بست؟ او اعداد یک تا صد را به ردیف پشت سرهم نوشت، سپس بار دیگر همین اعداد را بالعکس، این بار از صدتا یک، درست در ردیف زیرین اعداد قبلی نوشت. طوری که هر عدد زیر عدد ردیف بالاتر قرار گرفت.وی مشاهده کرد که مجموع هر کدام از ستون های به وجود آمده ۱۰۱ است. سپس نتیجه گرفت که صد تا عدد ۱۰۱ داریم که حاصل مجموع آنها می شود ۱۰۱۰۰=۱۰۱*۱۰۰. پس از آن تنها کافی بود که این مجموع به دست آمده نصف شود یعنی:
۵۰۵۰ = ۲ / ۱۰۱۰۰
شاید «شارل فردریک گاوس» شاگرد با ذکاوت کلاس که این روش جالب را به کاربرد، آن هنگام نمی دانست، روش بسیار کارا و مفیدی را برای جمع بستن رشته ای از اعداد ارائه داده است که تا سالیان سال مورد استفاده ریاضیدانان خواهد بود.اکثر مفاهیم ریاضی به قدری با زندگی روزمره ما گره خورده است که تمام مردم بدون آگاهی داشتن و واقف بودن به آن، از کنارش می گذرند و تنها کاربر خوبی هستند و بس!

نویسنده:علی عرب

تعداد قطرهای یکnضلعی محدب

نویسنده : هادی سیف آبادی

یک کاغذ را چند بار میتوان تا کرد

شاید تا کنون شده باشد که در مواقعی که بیکار هستید یا اینکه انتظار خبر مهمی را می کشید برای سرگرم کردن خودتان کاغذی را که در اطرافتان هست بردارید و شروع به تا کردن آن کنید و بعد از چند بار متوجه شوید که دیگر نمی شود کاغذ را تا کرد. در این صورت یا از تا کردن کاغذ منصرف می شوید یا آن را باز می کنید و دوباره شروع به تا کردنش می کنید... البته ممکن است قبل از اینکه به آن زمان برسید خبر مهم به شما داده شود و کاغذ را به جای اولش برگردانید !!! 

این مسئله را همه ما تجربه کرده ایم اما شاید هیچ کدام از ما به طور جدی روی آن فکر نکرده باشیم. 

اگر ورق را هر بار طوری تا کنید که اندازه آن نصف شود بیش از 7 یا 8 بار نمی توانید آن را تا کنید. مهم نیست ورق اولیه شما چقدر بزرگ باشد. شاید تا به حال این قضیه را شنیده باشید و سعی کرده باشید که آن را امتحان کنید و متوجه شده باشید که تا کردن کاغذ بیش از7 یا 8 بار بسیار سخت است. آیا می توان گفت که این اعداد یک محدودیت مستدل و عمومی برای تا کردن کاغذ هستند؟ 

فرض کنید شما کاغذی را انتخاب کرده اید که دارای پهنای w و ضخامت t است . اگر شما شروع به تا کردن ورق از یک سمت بکنید وقتی به جایی برسید که دیگر نتوانید کاغذ را تا کنید یک نوار باریک خواهید داشت. 
با هر تا کردنی ضخامت کاغذ دو برابر می شود و پهنای آن نصف خواهد شد. یعنی بعد از N بار تا کردن ضخامت خواهد بود و البته مشخص است که پهنا می شود و نسبت ضخامت به پهنا برابر می شود. 
اگر با کاغذی به پهنای 11cm و ضخامت 0.002cm این کار را انجام دهید بعد از 7 بار تا کردن نسبتt/w برابر 1/6 می شود. این بدان معنیست که اندازه ضخامت از پهنا بیشتر می شود و در نتیجه دیگر قادر به تا کردن کاغذ نخواهید بود. اگر این کاغذ را 50 بار بزرگتر کنید شاید بتوانید آن را تا 10 بار هم تا کنید. 

اگر به صورت متناوب کاغذ را از عرض و طول تا کنید ممکن است تعداد دفعات بیشتری بتوانید به تا کردن کاغذ ادامه دهید. در این صورت هر بارضخامت دو برابر می شود در صورتی که پهنا هر دو دفعه یک بار نصف می شود. 

چندین سال پیش هنگامی که بریتنی گالیوان در دبیرستان درس می خواند با این مسئله رو به رو شد که چگونه کاغذی زا 12 بار تا کند . او باید برای گرفتن نمره از یکی از کلاسهایش این مسئله را حل می کرد. بعد از آزمایش راه های مختلف او موفق شد که ورقه نازکی از طلا را 12 بار تا کند. اما مسئله طرح شده در باره کاغذ بود و نه طلا. 

گالیوان بر روی معادله تعداد دفعاتی که می توان یک کاغذ با اندازه معین را تا کرد کار کرد. 



که در آن L کمترین درازای کاغذ، t میزان ضخامت کاغذ و n تعداد دفعاتی است که می توان کاغذ را تا کرد. واحد t و L باید یکسان باشد. 

برای یک طول و ضخامت معین عبارت بیانگر آن است که صفحه بعد از n بار تاکردن چند برابر کوچک شده است. با n=0 شروع می کنیم و به همین ترتیب به رشته ای از اعداد به این صورت می رسیم: 

0, 1, 4, 14, 50, 186, 714, 2794, 11050, 43946, 175274, 700074, 2798250, . . . 

این به این معنی است که در تای دوازدهم 2798250 برابر مقدار کاغذی که در تای اول از دست می رود از دست خواهد رفت. 

گالیوان در کتابی با نام Historical Society of Pomona Valley چگونگی به دست آوردن این معادله و تلاشش برای حل مشکل را توضیح داده است. بالاخره در June 2002 گالیوان یک کاغذ بزرگ را 12 بار تا کرد.

نویسنده:علی عرب

20 نکته در یادگیری ریاضیات

 

برای آنکه بتوانید ریاضی را بهتر بخوانید، بهتر بفهمید،

بهتر یاد بگیرید و بیشتر با آن دوست شوید بیست نکته

 زیر را بخوانید و به کار ببرید.

۱-به خاطر داشته باشید که یادگیری درس ریاضی حتما

باید در کلاس انجام گیرد زیرا یادگیری این درس به شدت

وابسته به معلم است.

۲- برای یادگرفتن ریاضیات داشتن تمرکز الزامی است.

 پس به هنگام یادگیری سر تا پا گوش باشید. به ویژه

 اینکه دبیر ریاضی از معدود دبیران پشت به کلاس است

 زیرا دائما مجبور به استفاده از تخته برای نوشتن است.

۳- به توضیحات دبیر یا مدرس ریاضی باید کاملا دقت کنید

 زیرا چکیده ی چند سال تجربه و انتقال مطلب به همراه

منطبق ریاضیاتی درس را تواما ارائه می کند.

۴- مراحل محاسباتی هر تمرین را به زبان خودتان برای

 خودتان بازگویی کنید و راهنما و خود آموز خاص خودتان

 را در هر مبحث بنویسید.

۵- از عدم توانایی یا مهارتتان در حل تمرینها و مسائل

 نترسید و دلسرد نشوید بلکه با شعف تمام با آن برخورد

 کنید زیرا با پی بردن به ضعف ها و نقص هایتان نیمی

از عیب را رفع کرده اید.

۶- به هنگام حل تمرین حدس بزنید که چگونه سؤال یا

سؤالات مشابهی ممکن است در امتحان بیابید.

۷- در انجام تمرینهای هندسه، درک این که قضیه از

شما چه چیزی را می خواهد، مهم است. هر چه

راههای بیشتر و جدیدتری برای بیان محتوای قضایا،

 تعاریف و اصول موضوعه پیدا کنید، هندسه را بهتر فهمیده اید.

۸- ریاضی سیری پلکانی دارد.بنابراین آمادگی مهارتی

 در انجام مفاهیم قبلا آموخته شده و درک آنها پیش نیاز

 درک مفاهیم ریاضی بعدی است.

۹- در کلاس درس ریاضی فعال باشید. دقت کنید، سؤال

کنید تمرین کنید، مراحل محاسباتی را ثبت کنید.

۱۰-موقع یادگیری تلاش کنید ساختار ریاضی، ارتباطات،

 روابط اجزاء و منطبق ریاضی حاکم بر آن، کاربردها و سایر

 ویژگی های نظری مطلب را بفهمید.

۱۱- با خودسنجی در تمرین های ریاضی، بلافاصله علل

ناکامی و عدم موفقیت خودتان در مقابله با تمرین را

ریشه یابی کنید مثلا این ناکامی ناشی از این باشد که:

الف) در درک و فهم ریاضیاتی تمرین مورد نظر مشکل دارید.

ب) در حل تمرین یا تمرین های مورد نظر مشکل دارید.

ج) تمرین هایی که انجام داده اید به حد کفایت و لازم نبوده است.

۱۲- تمرین های ریاضی را یک ضرورت و نه اجبار تلقی کنید

 و با داشتن نگرش مثبت به این تکالیف و هدفمند بودن از

 تمرین های ریاضی استفاده بیشتری ببرید.

۱۳- فقط به تمرین های موجود در کتاب درسی بسنده

نکنید بلکه از کتاب های ویژه حل تمرین یا به اصطلاح

کتاب کار هم استفاده کنید.

۱۴- اصل اساسی در انجام تمرین های ریاضی استفاده

 از استدلال قیاسی است نسبت به این مساله حساس

 و واقف باشید تا سرعت کارتان زیاد شود.

۱۵- هیچ گاه به هنگام خستگی به ادامه تمرین ریاضی

 نپردازید زیرا خستگی باعث کاهش دقت و تمرکزتان

شده و ضریب خطاها و ناکامیتان را بالا می برد.

۱۶- ریاضی مثل هر علم دیگری زبان خاص خودش را دارد.

 این زبان را بفهمید و بیاموزید تا از ارتباط با ریاضی لذت

 بیشتری ببرید. زبان ریاضی مجموعه ای از اعداد، علائم

و نمادها، حروف، اشکال و روابط بین آنهاست.

۱۷- یکی از موانع درک ریاضی، نداشتن تصور ریاضیاتی

 مثبت از خود است. این موانع ممکن است در درک

ریاضی، در تمرین ریاضی، در امتحان ریاضی دادن یا در

 تست ریاضی زدن باشد. با تلاش و تمرین سعی کنید

 بر این موانع غلبه کنید.

۱۸-اصول حل مساله را یاد بگیرید و به کار ببرید. این

اصول شامل موارد زیر است:

۱) مساله را بفهمید. یعنی فرض ها و شروط مسأله

 را درک کنید. داده ها و مجهول ها را روی کاغذ بیاورید،

ترسیم کنید یا مجسم کنید.

۲) ارتباط منطقی میان داده ها، شروط مسأله و مجهول

 را پیدا کنید.

۳) راه حل ها را پیدا کنید.

۴) عملیات را اجرا کنید و محاسبات لازم را انجام دهید.

۵) جوابهای به دست آمده را وارسی کنید و از صحت آنها

مطمئن شوید.

۶) راه حل های کوتاه تر یا متفاوت را پیدا کنید.

۱۹- هرگز قبل از حصول اطمینان از یادگیری متن و

جوهره ی درس به سراغ انجام تمرین نروید زیرا احتمال

ناکام شدن و عدم موفقیت تان زیاد خواهد بود.

۲۰- هرگز به سراغ حل المسائل نروید مگر آنکه قبلا:

۱-کتاب درسی را خوانده باشید.

۲-جزوه درسی تان را دقیق مطالعه کرده باشید.

۳-از کتاب کمک درسی یا نوار یا سی دی آموزشی

 استفاده کرده باشید.

۴-از معلم تان برای رفع اشکال کمک گرفته باشید.

۵-به دوستانتان یا همکلاسی های برتر برای رفع اشکال

 مراجعه کرده باشید.

۶-از اعضاء خانواده یا دیگران کمک گرفته باشید.

موفق باشید.

نویسنده:علی عرب

زنبورها و ریاضیات!!!

یک، دو، سه! اگر شما زنبور عسل بودید، می‌توانستید تا عدد سه را بشمارید!

 

دانشمندان متوجه شدند که زنبورها، تنها حشره‌هایی هستند که قادرند تعداد شیء‌هایی که در اطرافشان است (کمتر از سه) را تشخیص بدهند. علاوه بر زنبورها، دلفین‌ها و کبوترها و راکون‌ها این توانایی را دارند، اما کشف این استعداد در یک حشره و با توجه به ساختار ساده بدنی‌اش، باعث تعجب دانشمندان شده است. ----البته مبنای تشخیص زنبورها، از روی شمارش شیءها نیست، بلکه آنها بر اساس عادت می‌توانند ارتباط بین چیزهایی که زیاد می‌بینند را تشخیص دهند. مثلاً اگر سه گل در نزدیکی‌شان باشد، آنها می‌توانند «سه» های دیگر را تشخیص بدهند.

---

یک دانشمند استرالیایی که نزدیک 30 سال است روی زندگی زنبورها تحقیق می‌کند، با ارائه آزمایشی به این ویژگی عجیب پی برده است. او تعداد 20 زنبور را از مسیر تونل مانندی که در آن دو لکه آبی رنگ قرار داشت، عبور داد. در انتهای این تونل، دو خروجی وجود داشت که بالای یکی از آنها دو لکه آبی و بالای خروجی دیگر سه لکه آبی قرار گرفته بود. اگر زنبور مسیری را که دو لکه آبی داشت انتخاب می‌کرد، به یک ظرف پر از شکر می‌رسید و در غیر این صورت چیزی نصیبش نمی‌شد! نتیجه این آزمایش که به اصطلاح به آن «شرطی کردن» می‌گویند، شگفت انگیز بود؛  70 درصد زمان ها زنبورها به ظرف شکر رسیدند! این مسئله نشان داد که زنبورها قادرند تعداد شیء را تشخیص بدهند. البته تحقیق‌های دانشمندان به همین جا ختم نشد، بلکه آنها زنبورها را مورد آزمایش‌های سخت‌تری قرار دادند. در آزمایش اول رنگ را تغییر دادند، یعنی دو لکه زرد رنگ در تونل و دو لکه آبی رنگ در سر راه خروجی قرار دادند. در آزمایش دیگری علاوه بر رنگ، نوع شکل را هم متفاوت انتخاب کردند. یعنی زنبورها می‌بایست پس از دیدن تصویر سه ستاره آبی، به سمت خروجی دارای سه برگ سبز می‌رفتند تا عسل نصیبشان شود! با انجام آزمایش دیگری که در آن چهار علامت قرمز در ابتدای مسیر قرار داشت، دانشمندان دریافتند که زنبورها نمی توانند تعداد چهار را الگو قرار بدهند و به دنبال شکل‌های چهارتایی دیگری بگردند. البته تا اینجا هم زنبورها نشان دادند که حشره‌های بسیار باهوشی هستند و نباید آنها رادست کم گرفت!

نویسنده:علی عرب

ضرب المثل های ریاضی

ما صد نفر بودیم, ان ها دو نفر بودند همراه

در زمان قاجاریه یک فوج سرباز مامور سرکوب یک عده اشرار شدند .
 در عرض راه همین که لشکر به گردنه ای رسید دو نفر دزد از ترس جان خود به ان ها حمله وشلیک کردند. 
 سربازان براثرظلم و فساد حاکم برمملکت انگیزه و شجاعتی برای جنگیدن نداشتندازشدت وحشت وترس تفنگها را بر زمین  ریختندو دست ها را بالا بردند و تسلیم گردیدند.
 دزدان چون این دیدند بر جسارتشان افزودندو فرود امدندو تمام نقدینه و اشیا سبک وزن و سنگین قیمت شان را برداشتند واز پی کارشان رفتند.
وقتی این خبر به سلطان رسید سربازان را احضار کردو از ان ها با خشم وغضب پرسید:چگونه دو نفر دزد توانستندشما صد سربازمسلح را لخت کنند؟
اندام تمامی سربازان به لرزه افتاده بودوازجواب وامانده بودندامایک نفرکه جرات بیشتری داشت درجواب گفت:
قربان ما صد نفر بودیم تنها, آن ها دو نفر بودند همراه

                                            دوقرت ونیمشم باقیه

گویند سلیمان نبی با جانوران در ارتباط بوده. روزی مجموع جانوران دنیا را به ضیافت خواند  پیش از همه ماهی بیرون اورد وقسمت خویش یا قورباغه ای سر از آب از سفره عام بخواست. سهمش را به او دادند بخورد و باز طلب کرد بدادند و او دوباره خواستارشدتا آنگاه که تمام آمادگی ها و تشریفات جشن به کاراو رفت وجانورهم چنان ازمند بود سلیمان در کار او ماندو پرسید: 
رزق تو روزانه چه مقدار است؟
گفت:سه جرعه که اکنون نیم جرعه ی ان مرا داده اند و منتظر دو نیم جرعه ی دیگر هست.
 این مثل را در مورد افرادی به کار می برند بسیار طمع کارند و هرچه به آن ها دهیم شاکر نمی شوند

  دو بلا در یک زمان
منصور دوانیقی,به یکی از اعراب گفت:شکر خدا را به جای بیاورید که چون حکومت شما به من واگذارشدطاعون از بلاد مرتفع گردید.
عرب گفت:خدای بلند مرتبه از آن عادل تر است که دو بلا را هم زمان بر بندگانش بفرستد. منصور از این سخن خجل و شرمگین شد و کینه ی ان مرد را به دل گرفت تا بالاخره او را کشت.

  صد تومن را می دادم که بچه ام یک شب بیرون نخوابه

مردی را فرزند گم شد. منادی پشت منادی به کوی و برزن فرستاد و هرساعت مژده یابنده را افزایش می دادو تانزدیک
غروب مژده گانی به100 تومان رسید 
آن که کودک را یافته بود, گمان کردکه هرچه در دادن طفل دیر کند,مژده گانیش بیشتر می شود.چون صبح شد اثری از منادیان ندید ناچار خود نزد پدر رفت مطالبه 100 تومان
مژدگانی را کرد.
پدر گفت: 100تومان را زمانی میدادم که بچه ام یک شب بیرون نخوابد.

نویسنده:علی عرب

ریاضی دان ها خوشبختر می شوند!

به گزارش خبرنگار علمی باشگاه خبرنگاران، پزشکان با بررسی حدود 17000 نفر در یک آزمایش در طول حدود 50 سال دریافته اند که مهارت های ریاضی و درک زبان قوی تر در کودکان در سنین 7 سالگی سبب موفقیت بیشتر آنها در زندگی می شود.

گفتنی است، این افراد انسان های خونسردتر و مهربان تر و  همینطور به لحاظ اقتصادی موفق تر بودند، همینطور در حفظ سلامتی خود کوشاتر بودند.

پزشکان امیدوار هستند تا با استفاده از این روش بتوانند تداخلات ژنتیکی بین دوقلوها را تشخیص دهند.

پزشکان به والدین توصیه می کنند تا به ویژه در سن 7 سالگی سعی کنند با مهربانی و تشویق و حمایت کودک خود را به درس خواندن و یادگیری بهتر ریاضیات برای تکامل بهتر مغز او در بزرگسالی اقدام نمایند.

نویسنده:علی عرب

آموزش تصویری مجموع زاویه های داخلی مثلث

نویسنده : هادی سیف آبادی

کی گفته دو دو تا نمیشه پنج تا

برای دیدن اثبات دودوتا پنج تا به ادمه مطلب بروید

هفت سین ریاضی

محمد دارابی

عجایب عدد 7

*رنگین کمان 7 رنگ دارد .

*عجایب جهان 7 تا هستند .

* سوره حمد که اولین سوره قرآن است 7 آیه دارد .

* آسمان 7 طبقه دارد .

*موسیقی ایران و یونان 7 دستگاه دارد .

* 7 نوع ساز بادی وجود دارد .

* 7 نت موسیقی وجود دارد .

* ایرانیان برای اهورامزدا 7 صفت نیک بر می شمردند .

* سفره سال نو 7 س دارد .

* عرفای بزرگ برای عشق و وصال 7 مرحله طی می کنند .

* طواف نیز 7 بار است .

نویسنده:علی عرب

ضرب ذهنی عددهای دو رقمی از 10 تا 20

محمد دارابی

پاور پوینت عجایب ریاضی

برای دانلود کلیک کنید

حجم فایل : 749kb


نویسنده : محمد دارابی

چرا ۱ “یک” ــه؟ چرا ۲ “دوئـــه” و….

چند نکته ی جالب مربوط به ریاضی

1.در ساعت 12 و 34 دقیقه ی روز پنجم ماه مه (87/6/5) اعداد نشن دهنده ی زمان به صورت 12345678 پشت سر هم قرار خواهد گرفت.
این حالت تا سال 2078 میلادی تکرار نخواهد شد

2.بزرگ ترین عدد شناخته شده در ریاضی (سانتیلیون) است.
این عدد از رقم 1 با 600صفر در جلوی ان تشکیل شده است.

3.یک گروه ریاضی دان فرانسوی به نا (نیکلوس بورباکی) بر روی دایره المعارفی به نام (ارکان ریاضیات)کار کرده اند.
در این دایره المعارف 200 صفحه فقط در مورد عدد 1 و موضوعات مرتبط با ان نوشته شده است.

4.بزرگ ترین عددی که با سه رقم میتوان نوشت 9 به توان 9 به توان 9 میباشد.این عدد دارای 369 میلیون رقم میباشد که برای خواندن ان سالها وقت لازم است.

5.دو عدد وجود دارند که هم اگر با هم ضرب شوند و هم اگر از هم کم شوند جوابشان یکی خواهد بود
این دو عدد 19 و 0/95 می باشند.

نویسنده:علی عرب

ارتباط موسیقی و ریاضیات

لیبنیز

شاید درباره ارتباط علوم مطالبی شنیده باشید اما آیا تا کنون درخصوص وجود ارتباط بین علوم و هنر اندیشیده اید ؟

نمونه ای از این ارتباط رابطه بین موسیقی و ریاضیات است. هنگامی که در این زمینه شروع به تحقیق کنید، احتمالا با نام فیثاغورث ، موزارت و باخ بیشتر از دیگران مواجه خواهید شد . اما اولین کسی که به این ارتباط پی برد ، فیثاغورث ، فیلسوف و ریاضیدان یونانی بود. نام این دانشمند بزرگ بی شک ما را به یاد رابطه معروفش در مثلث قائم الزاویه می اندازد. اما او در زمینه موسیقی نیز فعالیتهایی داشته است. بسیاری از دانشمندان او را پدر علم و بعضی از موسیقیدانان پدر موسیقی میدانند. شاید تعریف او از موسیقی بعد از گذشت بیست و شش قرن ، هنوز یکی از زیباترین تعاریف باشد :

عدد پی

نویسنده : محمد دارابی

کشف جدید ترین و طولانی ترین عدد اول جهان

دانشمندان و ریاضی دانها همیشه به دنبال راه هایی هستند تا تئوری ها را اثبات یا رد کنند و یا دامنه تازه ای از علم را معلوم نمایند که تا کنون در تاریکی قرار داشته است. آن گونه که به نظر می‌آید، تحقیق هیچ گاه پایانی نخواهد داشت و همیشه کشفیات جدید در راه هستند.
 محققان Curtis Cooper از دانشگاه مرکزی میسوری به تازگی بزرگترین عدد اول جهان را کشف کرده اند. این عدد اول که محققان توانسته اند آن را محاسبه کنند، از ۱۷،۴۲۵،۱۷۰ رقم تشکیل شده است.
 آنها این کشف را با استفاده از برنامه Great Internet Mersenne Prime Search یا GIMPS انجام داده‌اند. این پروژه یک شبکه از کامپیوترهای شخصی در سراسر دنیا است که به صورت اختصاصی برای تحقیقات در خصوص اعداد اول مورد استفاده قرار می گیرد. عدد کشف شده توسط تیم کوپر، 2 به توان 57,885,161 منهای 1 است.
اهمیت چنین کشفی این است که عدد مورد نظر، اولین عدد اول کشف شده طی چهار سال گذشته است. یافتن یک عدد اول جدید بسیار به ندرت اتفاق می افتد و ریاضی دان ها پیدا کردن آن را به یافتن الماس تشبیه می کنند. برای اینکه تصوری از این عدد داشته باشید، بهتر است بدانید فایل متنی حاوی آن ۲۲ مگابایت حجم دارد. در حالی که این فایل تنها حاوی توالی اعداد پشت سر هم است.
 اگر ریاضیات دوران مدرسه را به خاطر داشته باشید، می دانید که اعداد اول تنها بر خودشان و بر عدد یک قابل تقسیم هستند. دیگر نکته جالب داستان اینجا است که ۱۴عدد اول بزرگی را که فعلا می‌شناسیم، همگی توسط پروژه GIMPS کشف شده اند.

نویسنده:ابوالفضل امیدی

استفاده از عدد پی در دوره هخامنشیان!

مهندسان هخامنشی راز استفاده از عدد پی (۳/۱۴ ) را دو هزار و پانصد سال پیش کشف کرده بودند. آنها در ساخت سازه های سنگی و ستون های مجموعه تخت جمشید که دارای اشکال مخروطی است، از این عدد استفاده می کردند.

باقی در ادامه مطلب

فرمول ریاضی یک فنجان چای مطبوع:

TB+ (H2O) 2mins BT+ C(10 ml) 6 mins BT= PC(OT 60°c

توضیح علائم اختصاری:

TB یک چای کیسه ای

BT زمان دم کردن/ در این فرمول دو دقیقه

 H2O آب

C شیر/ در این فرمول 10 میلی لیتر

PC یک فنجان چای مطبوع

OT دمای مناسب برای نوشیدن چای/ در این فرمول 60 درجه سانتیگراد

نویسنده : هادی سیف آبادی

شگفتی ها وزیبایی های ریاضی

نویسنده : هادی سیف آبادی

 

 

1x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111

 

9x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

 

شگفت انگیز بود ، نه ؟ 

 

حالا تقارن را ببینید :

1x 1 = 1
11x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111= 12345678987654321 

 

حالا توجه کنید :

اگر حروف الفبای انگلیسی را :

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

بترتیب بصورت زیر در نظر بگیریم :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26

کلمه ی :                            H-A-R-D-W-O-R-K 

معادل خواهد بود با :   8+1+18+4+23+15+18+11 = 98% 

 

کلمه ی :                           K-N-O-W-L-E-D-G-E

معادل خواهد بود با :   11+14+15+23+12+5+4+7+5 = 96%  

 

اما کلمه ی :                          A-T-T-I-T-U-D-E

معادل خواهد بود با :    1+20+20+9+20+21+4+5 = 100%

 

حالا توجه کنید به :                  L-O-V-E-O-F-G-O-D

که مساوی می شود با :  12+15+22+5+15+6+7+15+4 = 101%

شگفتی ها و زیبایی های توان

به تساوی زیر نگاه کنید :

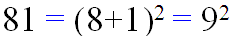
بله ۸۱ برابر است با توان دوم ِ مجموع ارقامش.

آیا اعداد دیگری با این ویژگی وجود دارند؟

به عدد زیر نیز توجه کنید :

حتما ً شگفت زده شده اید !

در این قسمت می خواهیم اعدادی را معرفی کنیم که این اعداد با توانی از مجموع  ارقامشان برابرند. البته در این میان، اعداد یک رقمی با مجموع ارقامشان به توان ۱ برابند و از آن ها چشم پوشی می کنیم. یافتن اعداد کوچک با این ویژگی کار ساده ای است اما یافتن اعداد بزرگتر بسیار مشکل و زمان بر خواهد بود. در جدول زیر تعدادی از این اعداد را به نمایش در آورده ایم . ببینید و لذت ببرید :

	=	عدد
۹۲	=	۸۱
۸۳	=	۵۱۲
۱۷۳	=	۴۹۱۳
۱۸۳	=	۵۸۳۲
۲۶۳	=	۱۷۵۷۶
۲۷۳	=	۱۹۶۸۳
۷۴	=	۲۴۰۱
۲۲۴	=	۲۳۴۲۵۶
۲۵۴	=	۳۹۰۶۲۵
۲۸۴	=	۶۱۴۶۵۶
۳۶۴	=	۱۶۷۹۶۱۶
۲۸۵	=	۱۷۲۱۰۳۶۸
۳۵۵	=	۵۲۵۲۱۸۷۵
۳۶۵	=	۶۰۴۶۶۱۷۶
۴۶۵	=	۲۰۵۹۶۲۹۷۶
۱۸۶	=	۳۴۰۱۲۲۲۴
۴۵۶	=	۸۳۰۳۷۶۵۶۲۵
۵۴۶	=	۲۴۷۹۴۹۱۱۲۹۶
۶۴۶	=	۶۸۷۱۹۴۷۶۷۳۶
۱۸۷	=	۶۱۲۲۲۰۰۳۲
۲۷۷	=	۱۰۴۶۰۳۵۳۲۰۳
۳۱۷	=	۲۷۵۱۲۶۱۴۱۱۱
۳۴۷	=	۵۲۵۲۳۳۵۰۱۴۴
۴۳۷	=	۲۷۱۸۱۸۶۱۱۱۰۷
۵۳۷	=	۱۱۷۴۷۱۱۱۳۹۸۳۷
۵۸۷	=	۲۲۰۷۹۸۴۱۶۷۵۵۲
۶۸۷	=	۶۷۲۲۹۸۸۸۱۸۴۳۲
۴۶۸	=	۲۰۰۴۷۶۱۲۲۳۱۹۳۶
۵۴۸	=	۷۲۳۰۱۹۶۱۳۳۹۱۳۶
۶۳۸	=	۲۴۸۱۵۵۷۸۰۲۶۷۵۲۱

نویسنده : هادی سیف آبادی

عجیب ترین جمله در زبان انگلیسی که با ریاضی هم بی ربط نیست!

عجیب‌ترین جمله در زبان انگلیسی!!! 

این جمله با کلمه ای یک حرفی آغاز می شود٬ کلمه دوم دو حرفیست٬‌ چهارم چهار حرفی تا بیستمین کلمه بیست حرفی: 

 

I do not know where family doctors acquired illegibly perplexing handwriting nevertheless, extraordinary pharmaceutical intellectuality counterbalancing indecipherability, transcendentalizes intercommunications incomprehensibleness 

ترجمه جمله : 

نمیدانم این دکترهای خانوادگی این دست خطهای گیج کننده را از کجا کسب میکنند. با این حال سواد پزشکی انها غیر قابل کشف بودن این دست خط ها را جبران کرده و بر غیر قابل .

دنباله ی اعداد فیبوناچی

در دوران حیات فیبوناچی مسابقات ریاضی در اروپا بسیار مرسوم بود در یکی از همین مسابقات که در سال ۱۲۲۵ در شهر پیزا توسط امپراتورفردریک دوم برگزار شده بود مسئله زیر مطرح شد:

«فرض کنیم خرگوش‌هایی وجود دارند که هر جفت (یک نر و یک ماده) از آنها که به سن ۱ ماهگی رسیده باشند به ازاء هر ماه که از زندگی‌شان سپری شود یک جفت خرگوش متولد می‌کنند که آنها هم از همین قاعده پیروی می‌کنند حال اگر فرض کنیم این خرگوشها هرگز نمی‌میرند و در آغاز یک جفت از این نوع خرگوش در اختیار داشته باشیم که به تازگی متولد شده‌اند حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت.»

حال اگر تعداد خرگوش ها را در ماههای اول و دوم و ... حساب کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است.

۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴,…

فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفت‌انگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضی‌دانان بلکه دانشمندان بسیاری از رشته‌های دیگر را به خود جلب کرده است.

بازنگاری نقشه‌ی جهان با استفاده از ریاضیات، منجر به خلق پدیده‌ای زیبا شده است

تصویری که امروزه از کره‌ی زمین بر اذهان یکایک ما نقش بسته، غالباً تصویری از مرزهای سیاسی میان کشورها است. این تصویر که برخی اوقات ناراحت‌کننده و زشت به نظر می‌رسد، باعث شده تا به سختی بتوانیم ذهنیت خود از این کره‌ی آبی – خاکی را تغییر دهیم. برای چند ثانیه تصور کنید چه اتفاقی می‌افتاد اگر کشورها به جای دخالت در کار یکدیگر، تنها پایتخت و شهرهای نزدیک به پایتخت خود را کنترل می‌کردند. نقشه‌ی فوق با الهام گرفتن از این ایده و با استفاده از ریاضیات تهیه شده است.

پیاده‌روی یک سال نوری چه قدر زمان و چند جفت کفش می‌خواهد؟

در صورتی که فرد برای هر مایل 80 کالری بسوزاند، برای طی یک سال نوری به دو تریلیون PowerBar نیرو نیاز دارد.

 چنانچه شخص سفر خود را پیش از عصر دایناسورها آغاز می‌کرد، طی کردن این میزان مسافت احتمالا تا زمان حال طول می‌کشید.

یک سال نوری مسافتی است که نور در یک سال طی می‌کند و واحدی است که برای اندازه‌گیری فضای بین‌ستاره‌ای به کار می‌رود. سال نوری معادل 5.9 تریلیون مایل است.

در صورتی که فردی یک مایل را با سرعت متوسط در 20 دقیقه طی کند، حدود 225 میلیون سال زمان می‌برد تا سفر خود را کامل کند.

در صورتی هم که وی بر روی جت مافوق‌صوت Mach 9.68 X-43A ناسا (پرسرعت‌ترین هواپیمای جهان) سفر کند، طی کردن یک سال نوری، 95 هزار سال زمان می‌برد. طی‌کردن چنین مسافتی همچنین به انبوهی از کفش‌ها نیاز دارد.

یک جفت کفش ورزشی نوعی حدود 500 مایل دوام خواهد داشت، بنابرای برای طی این سفر، شخص به 11.8 میلیارد جفت کفش نیاز دارد.

نزدیک‌ترین ستاره به خورشید Proxima Centauri نام دارد که 4.22 سال نوری از زمین فاصله دارد، بنابراین رسیدن به این جرم کیهانی با چنین سرعتی برای یک شخص به زمانی باورنکردنی نیاز دارد.

قضیه چهار رنگ

قَضیه چهاررَنگیا حدس چهاررنگ از مسائل مشهور و قدیمی ریاضیات است که سال‌ها اثبات نشده مانده بود. به بیان ساده (و نادقیق) این قضیه می‌گوید:

برای رنگ کردن هر نقشه به طوری که کشورها و نواحی همسایه در نقشه هم‌رنگ نباشند فقط چهار رنگ کافی است.

سه رنگ برای نقشه های ساده تر کافیست ولی یک رنگ چهارم اضافی برای برخی نقشه ها لازم است. مثل نقشه هایی که در آن ها یک ناحیه با تعداد فرد نواحی دیگر احاطه شده است که به یکدیگر در یک دایره وصل هستند. قضیه 5 رنگ که اثباتی کوتاه و ابتدایی دارد، بیان می کند که 5 رنگ برای رنگ آمیزی نقشه کافیست . این قصیه در اواخر قرن 19 اثبات شده است(هیووو 1890). اثبات اینکه 4 رنگ کافیست بسیار سخت تر است. تعدادی اثبات های غلط و مثال های نقض از زمان ارائه قضیه 4 رنگ در 1852 بیان شده اند.

این مسئله به صورت معادله ابتدا درسال۱۸۵۲ عنوان شد و سرانجام در سال۱۹۷۶ با کمک رایانه  توسط کی اپپل و و. هیکن حل شد. این اولین قضیه مهمی بود که با استفاده از کامپیوتر به اثبات رسید. آنها نشان دادند که مجموعه ای از 1936 نقشه وجود دارد که هیچ کدام از آنها نمی توانند قسمتی از یکی از کوچکترین مثال نقض های قضیه چهار رنگ باشند. اپل و هیکن از یک برنامه کامپیوتری خاص منظوره استفاده کردند تا ثابت کنند هیچ کدام از این نقشه ها از این قاعده مستثنا نیستند. علاوه بر این هر نقشه ای فارغ از این که مثال نقض هست یا نه، حتما قسمتی را شامل می شود که شبیه یکی از آن 1936 نقشه می باشد و اثبات این نیاز به صدها صفحه تحلیل دست نویس بود. اپل و هیکن نتیجه گرفتند که اگر بخواهد کوچکترین مثال نقضی وجود داشته باشد باید شامل یکی از آن 1936 نقشه باشد. این تناقض به این معنی بود که هیچ مثال نقضی وجود ندارد و قضیه درست می باشد. در ابتدا اثبات آنها از طرف همه ریاضیدان ها مورد تایید واقع نشد، چرا که چک کردن یک اثبات کامپیوتری توسط انسان امکان پذیر نبود

عدد هفت

عدد هفت عددی است که شاید مثل همه ی عدد های دیگر در نظر ما عادی جلوه کند اما نگرش ما وقتی متبلور می شود که خواص عدد هفت را بدانیم و ببینیم چه «هفت» هایی در زندگی ما وجود دارند و ما در گیر و دار زندگی ماشینی و با بی تفاوتی از کنار آن ها رد می شویم مثلا شاید جالب باشد که بدانیم، رنگین کمان دارای هفت رنگ است .
عجایب جهان، هفت تا هستند.(که به عجایب هفت گانه معروفند ) یا در یونان باستان، اسطوره ای با نام هفت خدای، در ذهن مردم نقش بسته است، ویا شهر عشق، که دراشعار عطار آمده است، هفت شهر می باشد، سوره ی مبارکه حمد، که اوّلین سوره ی قرآن کریم است، هفت آیه دارد. آسمان دارای هفت طبقه است. بهشت وجهنم هر کدام دارای هفت طبقه و درجه هستند و طواف خانه خدا هفت دور است، موسیقی ایران و یونان هفت دستگاه داد، هفت نوع ساز بادی وجود دارد و علاوه بر این هفت نت موسیقی وجود دارد(دو، ر، می، فا، سل، لا، سی) و…

ریاضی زندگی

راه شگفت انگیز یادگیری ریاضی

دانشمندان دانشگاه آکسفورد با مطرح کردن یک ایده تعجب برانگیز اظهار داشتند که عبور جریان الکتریسیته از مغز در حین درس های ریاضیات می تواند مهارتهای عددی را تا یک سوم افزایش دهد.

 شرکت کنندگان در تحقیقات دانشگاه آکسفورد پس از عبور جریان الکتریسیته از مغزشان در محاسبات سریع تر شدند و توانایی یادگیری آنها پنج برابر بیشتر شد.

تیم تحقیقات دانشگاه آکسفورد به 51 دانشجو ریاضی آموزش داد و با عبور جریان الکتریسیته از مغز آنها، دانشمندان توانستند که مهارتهای عددی آنها را تا یک سوم افزایش دهد، آنها همچنین به این نتیجه رسیدند که مهارتهای محاسباتی شرکت کنندگان پنج برابر سریع تر شده است.

حدود نیمی از شرکت کنندگان، هنگام یادگیری یک جریان سبک از مغزشان عبور کرد، پس از پنج جلسه افرادی که از این فرآیند استفاده کرده بودند ارقام، جدول های زمانی و محاسبات را به سرعت به خاطر می آوردند که این سرعت و دقت درمقایسه با افرادی که تحت قرار گیری جریان الکتریسیته از مغزشان نبودند قابل توجه بود.

این افراد همچنین تا 30 درصد بیشتر توان محاسباتی داشتند. این درحالی است که این مهارت تا شش ماه بعد در آنها باقی ماند.

دکتر «روی کوهی کادوش» از کرسی روانشناسی آموزشی دانشگاه آکسفورد ابراز امیدواری کرد که این روش به افرادی که در ریاضیات مهارتی ندارد، کمک کند.

وی افزود: این تحقیق یک روش ارزان و مطمئن است که می تواند مهارتهای ریاضی افراد را با مداخله محدود ارتقا دهد. ما در این فرآیند آن بخش از مغز را که با ریاضیات سروکار دارد، تحریک کردیم چرا که مهارتهای ریاضی پایین برای بسیاری از افراد یک چالش محسوب می شود.این درمان بی درد و غیر تهاجمی است.

به طور تخمین یک نفر از هر پنج نفر با مهارتهای محاسباتی ابتدایی مشکل دارد این درحالی است که یک نفر از هر 15 نفر مبتلا به محاسبه پریشی (dyscalculia) است که این امر موجب می شود حتی شمارش برای آنها غیر ممکن باشد.

مشخص نیست که این تحریک الکتریکی چگونه عمل می کند اما اسکن های مغزی نشان می دهد که این امر ذخیره اکسیژن و مواد مغذی مغز را افزایش می دهد.

نتایج این تحقیق که در مجله بیولوژی امروز منتشر شده دربرگیرنده پنج جلسه 45 دقیقه ای ریاضی با حضور 25 نفر بوده که برای 20 دقیقه مغزشان با یک جریان الکتریکی سبک تحریک شده است.

این گروه اظهار داشت که این تحقیق می تواند موجب تغییر روش های جدید تدریس شده و بخش خفته مغز را که با اعداد سروکار دارد بیدار کند.

دکتر «کادوش» با اشاره به مسائل اخلاقی این تکنیک، اظهارداشت: هدف ما کمک به افرادی است که تواناییهای محدودی دارند البته این تکنیک می تواند به منظور ارتقای توانایی ها مورد استفاده افراد عادی یا فراتر از عادی نیز قرار بگیرد اما بحث درباره این این روش تقلب محسوب می شود یا خیر هنوز یک بخش باز است. اگر این روش در در دسترس همه قرار گیرد، ما آن را تقلب ارزیابی نمی کنیم .

محاسبه عجیب

از پدری پرسیدند: آیا درست است که می گویند:(زمانی فرا خواهد رسید که پسرها بزرگتر ازپدرشان خواهند شد؟)گفت:اتفاقا این موضوع سخت ذهن مرا به خود مشغول کرده است.

البته کاری به استعداد ونبوغ شان ندارم.منظور من سن وسال آنهاست.....

پرسیدند:به چه دلیل؟

گفت:به این دلیل که برایتان شرح خواهم داد.

وقتی پسرم متولدشد من۳۰ سال داشتم.یعنی ۳۰ برابر او سن داشتم.

وقتی ۲ ساله شدمن۳۲ سال داشتم.یعنی۱۶ برابراوسن داشتم.

وقتی۳ ساله شدمن۳۳ سال داشتم.یعنی۱۱ برابر او سن داشتم.

وقتی۵ ساله شدمن۳۵ سال داشتم.یعنی۷ برابر او سن داشتم.

وقتی۶ ساله شدمن۳۶ سال داشتم.یعنی۶ برابر او سن داشتم.

وقتی۱۰ ساله شدمن۴۰ سال داشتم.یعنی۴ برابر او سن داشتم.

وقتی۱۵ ساله شدمن۴۵ سال داشتم.یعنی۳ برابراو سن داشتم.

حالا او۳۰  ساله شده است ومن۶۰ سال دارم یعنی ۲ برابر اوسن دارم.

می ترسم اگر اوضاع به همین منوال پیش رود او به زودی ازمن جلو بزند و اوپدر من بشود و من پسر او بشوم! 

استخوان های نپر ( روش جذاب ضرب )

   

انیمیشن مثلث خیام پاسکال

زیبایــی و ریاضیــات

برج هانوی

مسئله برج هانوی به افسانه ای از هندوستان بازمی گردد. در یکی از معابد هندوستان سه ستون وجود داشته که در یکی 64 عدد حلقه به ترتیب قطرشان و جود داشته است. موبدان بر این باور بوده اند که هر گاه توانستند تمام این 64 حلقه را به به ستون سوم ببرند ، عمر جهان پیدا شده و دنیا به پایان خواهد رسید. بتا بر این موبدان دست به کار شدند و شروع به انتقال دادن حلقه ها کردند.

البته در این انتقال :

1- در هر جابجایی تنها یک حلقه را جابجا کنند

2- حلقه بزرگتر روی کوچکتر قرار نگیرد.

تعداد جابجایی ها به ازای n حلقه برابر 2ⁿ -1 جابجایی است . پس موبدان اگر در هر ثانیه یک حلقه را جابجا کنند باید 2⁶⁴ ثانیه یعنی تقریبا 584 بیلیون سال!!!