1)باقی مانده تقسیم هر عدد بر 2 یا 5 برابراست با باقی مانده تقسیم رقم سمت راست عدد بر 2 یا 5.
مثال :باقی مانده تقسیم عدد 7358 بر 5 برابر است با باقی مانده تقسیم عدد 8بر5 که برابر 3 میگردد.
2)باقی مانده تقسیم هر عدد بر 3یا 9 با باقی مانده تقسیم مجموع ارقام عدد بر 3 یا 9 برابر میباشد.
3)برای تعیین باقی مانده تقسیم هر عدد بر 11 کافی است ارقام عدد را از سمت راست به چپ بترتیب زوج وفرد نوشته و مجموع ارقام مکانهای فرد رااز مجموع ارقام مکانهای زوج کم کرده وباقی مانده عددحاصل رابر11 بدست می آوریم که همان باقی مانده تقسیم عدداولیه بر11 میباشد.
4) برای تعیین باقی مانده تقسیم هرعدد بر 7 یا 13 کافی است ارقام عدد رااز سمت راست به چپ سه رقم سه رقم جدا کرده و دسته های سه تایی را یکی درمیان اضافه وکم کرده و باقی مانده تقسیم عدد حاصل رابر 7یا 13 بدست می آوریم.
5)برای تعیین باقی مانده تقسیم هرعددبر 27 یا 37 کافی است ارقام عدد رااز سمت راست به چپ سه رقم سه رقم جداکرده و مجموع دسته های سه تایی رایافته وعدد حاصل رابر 27 یا 37 تقسیم می کنیم وباقی مانده حاصل همان باقیمانده تقسیم عدد اولیه بر 27 یا 37 میباشد.
6)عددی بر 4 بخش پذیر است که مجموع 2 برابر رقم دهگان ورقم یکان عدد بر 4 بخش پذیر باشد.
مثلا" :132 بر 4 بخش پذیر میباشدزیرا 8=2+3×2 بوده که بر 4 بخش پذیر است.
7)عددی بر 8 بخش پذیر است که مجموع چهار برابر رقم صدگان ودو برابر رقم دهگان ورقم یکان آن بر 8 بخش پذیر باشد.
نویسنده:علی عرب
۱۱
آبان
فارغ از ضرب و جمع و تفریق، حقایقی جالب و خواندنی در مورد ریاضیات وجود دارد که در زیر نمونه هایی از آنرا با هم میخوانیم…
یکی از مجموعه اعدادی که ما در علوم مختلف با آن سر و کار داریم اعداد رومی است ، در این پست ما به طور کامل به توضیح نماد های رومی و عدد نویسی آن میپردازیم.
رومی‌های قدیم برای نوشتن عددها از نمادهایی بدین شکل استفاده می‌کردند:
| نماد | I | V | X | L | C | D | M |
| عدد | ۱ | ۵ | ۱۰ | ۵۰ | ۱۰۰ | ۵۰۰ | ۱۰۰۰ |
آنها با پیروی از قانون‌هایی، با ترکیب این نمادها، نمادهای دیگری برای نمایش دیگر اعداد پدید آورده بودند. بعضی از این قانون‌های دستگاه عدد نویسی رومی، بدین شرح بوده است:
- هر نماد که در سمت راست نماد دیگر نوشته می‌شود، چنانچه مقدارش از آن نماد کمتر یا با آن مساوی باشد، ارزش آن نماد را زیاد می‌کند.
- III = ۱+۱+۱ = ۳
- XI = ۱۰+۱ = ۱۱
- VII = ۵+۱+۱ = ۷
- هر نمادی که در سمت چپ نماد دیگر نوشته می‌شود، چنانچه مقدارش از آن کمتر باشد، ارزش آن نماد را کم می‌کند.
- IV = ۵-۱ = ۴
- IX = ۱۰-۱ = ۹
- CD = ۵۰۰-۱۰۰ = ۴۰۰
- هرگاه نمادی بین دو نماد بزرگ‌تر از خود قرار گرفته باشد، ابتدا با نماد سمت راستش ترکیب می‌شود، یعنی از ارزش آن می‌کاهد و بعد، طبق قانون اوّل، تفاضل بر ارزش نماد دیگر اضافه می‌شود.
- XIV = (۵-۱)+۱۰ = ۱۴
- MCM = (۱۰۰۰-۱۰۰)+۱۰۰۰ = ۱۹۰۰
- برای اعداد بزرگ (
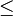۵,۰۰۰ ) در بالای هر نماد خطّی افقی قرار می‌گیرد که ارزش آن را ۱,۰۰۰ برابر می‌کند. مانند:(۵,۰۰۰ =
) - برای اعداد خیلی بزرگ ( 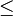۵,۰۰۰,۰۰۰
) شکل فراگیری وجود ندارد امّا گاهی آنها را با دو خطّ افقی در بالای نماد
یا با خطّی افقی در زیر نماد نمایش می‌دهند که ارزش آن نماد را ۱,۰۰۰,۰۰۰
برابر می‌کند. مانند:(۵,۰۰۰,۰۰۰ =
)
۰۳
اسفند